基数変換
コンピュータを学ぶ上で、2進数を理解することは、とても重要です。それは、コンピュータは、ONとOFFでデータを記憶しているからです。
記憶装置によって、ONとOFFを表現する方法は違います。例えば、5Vと0Vのように電圧で、あるいは、磁気の方向など、2つの異なる状態を作り出して、ONとOFFを表現しています。
ON ・・・ 1
OFF ・・・ 0
「ONを1」、「OFFを0」で表現するということは、2個の文字で数を表現することになります。つまり、コンピュータにとっては、10進数よりも2進数の方が扱いやすいため、コンピュータの内部では2進数を使っています。
ただし、人間にとって、2進数は扱いにくい表現になります。例えば、10進数の9を2進数で表すと1001になります。10進数で1桁で表現できたものが、2進数では4桁も必要になってしまいます。
このように2進数では、大きな数を表現すると桁数が非常に多くなってしまいます。また、この1と0の並びを覚えるのは大変です。そこで、8進数や16進数を使用して数値を表現する場合もあります。
基数変換表
| 10進数 | 2進数 | 8進数 | 16進数 |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
ネットワークの世界でも、2進数や8進数、16進数をつかって数値を表現します。ネットワーク機器は、コンピュータではないのになぜ?と疑問に思うかもしれません。
ネットワーク機器は、見た目はコンピュータに見えませんが、中身はコンピュータと変わりません。また、ネットワーク上のWebサーバなどの各種サーバもコンピュータであることに変わりありません。
そこで、ネットワークの世界においても、2進数や8進数、16進数を理解しておくことは、ネットワークを学習する上で重要になってきます。
IPアドレスは、10進数で表現しますが、内部的には2進数で扱われています。また、サブネットの概念には2進数は欠かせませんし、UNIX、Linuxのファイルのアクセス権であるパーミッションを指定する際には8進数が使われています。さらに、Cisco機器の動作を指定する際に設定するコンフィグレーションレジスタやMACアドレスは16進数で表現するようになっています。
ちなみにネットワークの世界では、小数をつかって数値を扱うことは、ほとんどありませんので、このサイトでは整数に限定して基数変換について解説していきます。
2進数から10進数
2進数の重みは、以下の図のようになっています。
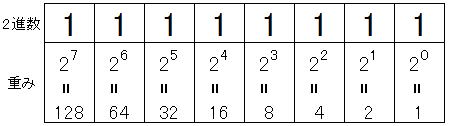
1のビットの立っているところの重みとを各桁の数字と掛けてからすべて足してゆけば、変換することができます。
例)(240)10→(11110000)2の基数変換
(注)(240)10は、10進数240を表します。
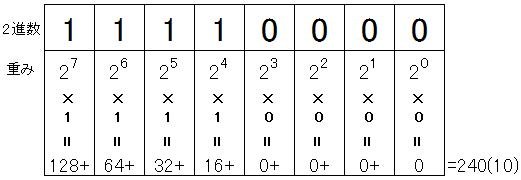
(11110000)2
= 1 × 27 + 1 × 26 + 1 × 25 + 1 × 24
+ 0 × 23 + 0 × 22 + 0 × 21 + 0 × 20
= 128 + 64 + 32 + 16 + 0 + 0 + 0 + 0
= (240)10
10進数から2進数
10進数から2進数に変換するには、10進数を2で除算した余りを並べて行き、出てきた余りを下から上に並べること変換することができます。
例)(240)10→(11110000)2の基数変換
(注)(240)10は、10進数240を表します。
2で割って余りを下から並べます。
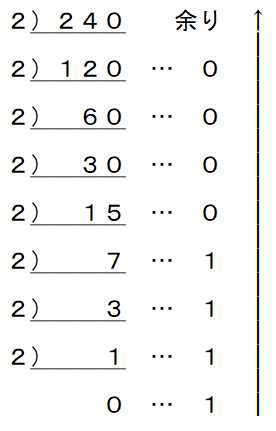
ネットワークの世界に関しては、10進数の0~255までの数値をよく扱います。それは、IPアドレスの表記が0~255で表現するからです。
10進数→2進数への基数変換に関しては、上の変換方法で求めることができますが、ネットワークの世界では、高々、0~255までの数値しか扱わないので各桁の重みで分解して考えた方が計算が楽かもしれません。
240=128+64+32+16
と重みで分解することができます。
128=27
64=26
32=25
16=24

重みに対応した所を1にすれば、2進数に変換することができます。
この変換方法に慣れれば、速く計算することができます。
10進数から8進数、10進数から16進数
10進数から8進数
10進数から8進数に変換するには、10進数を8で除算した余りを並べて行き、出てきた余りを下から上に並べることで変換することができます。
例)(240)10→(360)8の基数変換
(注)(240)10は、10進数240を表します。
8で割って余りを下から並べます。

10進数から16進数
10進数から8進数に変換するには、10進数を8で除算した余りを並べて行き、出てきた余りを下から上に並べることで変換することができます。
例)(240)10→(F0)16の基数変換
(注)(240)10は、10進数240を表します。
16で割って余りを下から並べます。

8進数から10進数、16進数から10進数
8進数から10進数
8進数の重みは、下図のようになっています。
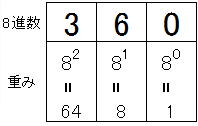
(360)8
= 3 × 82 + 6 × 81 + 0 × 80
= 192 + 48 + 0
= (240)10
16進数から10進数
16進数の重みは、下図のようになっています。
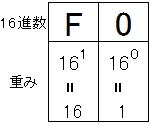
(F0)16
= 15 × 161 + 0 × 160
= 240 + 0
= (240)10
2進数から8進数、2進数から16進数
2進数から8進数
右から3桁ずつに分けます。足りないところは0で補います。
(11110000)2
= (011 110 000)2 ← 右から3桁ずつに分けます。
= (3 6 0)8
= (360)8
2進数から8進数
右から4桁ずつに分けます。足りないところは0で補います。
(111110000)2
= (0001 1111 0000)2 ← 4桁ずつに分けます。
= (1 F 0)16
= (1F0)16
8進数から16進数、16進数から8進数
8進数から16進数
(360)8
= (3 6 0)8
= (011 110 000)2 ← 各桁を2進数に変換します。
= (0000 1111 0000)2 ← 4桁ずつに分けます。足りないところは0で補います。
= (1111 0000)2 ← 上位の0を無視します。
= (F 0)16
= (F0)16
8進数から16進数
(F0)16
= (F 0)16
= (1111 0000)2 ← 各桁を2進数に変換します。
= (011 110 000)2 ← 3桁ずつに分けます。足りないところは0で補います。
= (3 6 0)8
= (360)8
サブネットマスクと2進数
ネットワークの世界では、IPアドレスを使って通信を行うのがデファクトスタンダードになっています。
このIPアドレスは、「xxx.xxx.xxx.xxx」という表記で、「xxx」の部分に10進数の「0~255」の4つの数値の組み合わせで表現します。例えば、「192.168.1.1」と表現します。
この10進数で表現されたIPアドレスを、場合によっては、2進数で解釈しなければならない時があります。
IPアドレスを使用するということは、2進数から10進数への変換、また、その逆の変換の計算を頻繁に行うようになることを意味しています。
例えは、下の2進数を10進数に変換する場合に下のように計算したのでは、効率が良いとは言えません。
(11110000)2
= 1 × 27 + 1 × 26 + 1 × 25 + 1 × 24
+ 0 × 23 + 0 × 22 + 0 × 21 + 0 × 20
= 128 + 64 + 32 + 16 + 0 + 0 + 0 + 0
= (240)10
IPアドレスの計算では、サブネットマスクという値を頻繁に使用するようになります。以下のサブネットマスクで使用する数値を暗記しておけば計算がとても楽になります。
※サブネットマスクの意味については、後のコンテンツで紹介してゆきます。
(11111111)2 = (255)10
(11111110)2 = (254)10
(11111100)2 = (252)10
(11111000)2 = (248)10
(11110000)2 = (240)10
(11100000)2 = (224)10
(11000000)2 = (192)10
(10000000)2 = (128)10
(00000000)2 = ( 0)10
また、上の数値を暗記しておけば、例えば193を2進数に変換する時も簡単です。
193 = 192 + 1
192を暗記していれば
(11000000)2 + (00000001)2 = (11000001)2
と計算することで、すぐに求めることができます。
