Radix conversion (binary, octal, hexadecimal)
Radix conversion
Understanding binary numbers is very important in learning computers. That’s because the computer memorizes data with ON and OFF. Different storage devices have different ways of expressing ON and OFF. For example, ON and OFF are represented by voltages such as 5V and 0V, or by creating two different states such as the direction of magnetism.
ON ・・・ 1
OFF ・・・ 0
Expressing “ON as 1” and “OFF as 0” means expressing a number with two characters. In other words, computers use binary numbers internally because binary numbers are easier to handle than decimal numbers.
However, for humans, binary numbers are a difficult representation to handle. For example, the decimal number 9 is 1001 in binary. A decimal number that can be expressed in one digit requires four digits in binary.
In this way, in binary numbers, the number of digits becomes very large when expressing large numbers. Also, remembering the sequence of 1s and 0s is difficult. Therefore, sometimes numbers are represented using octal or hexadecimal numbers.
● Radix conversion table
| Decimal number | Binary number | octal | Hexadecimal |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A. |
| 11 | 1011 | 13 | B. |
| 12 | 1100 | 14 | C. |
| 13 | 1101 | 15 | D. |
| 14 | 1110 | 16 | E. |
| 15 | 1111 | 17 | F. |
Even in the network world, numbers are expressed using binary, octal, and hexadecimal numbers. Why network devices are not computers? You may wonder.
Network equipment does not look like a computer, but inside it is the same as a computer. In addition, various servers such as web servers on the network are also computers.
Therefore, even in the network world, understanding binary, octal, and hexadecimal numbers is important for learning networks.
Although IP addresses are expressed in decimal numbers, they are handled internally in binary numbers. In addition, binary numbers are essential to the concept of subnets, and octal numbers are used to specify file permissions in UNIX and Linux. Furthermore, configuration registers and MAC addresses that are set when specifying the operation of Cisco devices are expressed in hexadecimal.
By the way, in the world of networks, it is rare to use decimals to handle numerical values.
Binary to Decimal
Binary weights are shown in the figure below.
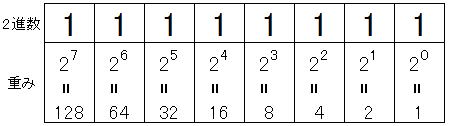
You can convert by multiplying each digit by the weight of the 1 bit and then adding them all up.
Example) (240) 10 → (11110000) Base conversion of 2
(Note) (240) 10 represents decimal number 240.
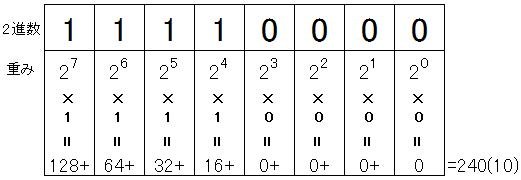
(11110000) 2
= 1 x 27 + 1 x 26 + 1 x 25 + 1 x 24
+ 0 x 2 3 + 0 x 2 2 + 0 x 2 1 + 0 x 2 0
= 128 + 64 + 32 + 16 + 0 + 0 + 0 + 0
= (240) 10
decimal to binary
To convert from a decimal number to a binary number, divide the decimal number by 2 and sort the remainders, then sort the remainders from bottom to top.
Example) (240) 10 → (11110000) 2Base conversion of
(Note) (240) 10 represents decimal number 240.
Divide by 2 and list the remainders from the bottom up.

When it comes to the network world, we often deal with numbers from 0 to 255 in decimal. That’s because the IP address notation is expressed from 0 to 255.
Regarding the radix conversion from decimal to binary, it can be obtained by the above conversion method, but in the world of networks, at most, only numbers from 0 to 255 are handled, so consider the weight of each digit. may be easier to calculate.
240 = 128 + 64 + 32 + 16
and can be decomposed by weights.
128=2 7
64=2 6
32=2 5
16=2 4

If the place corresponding to the weight is set to 1, it can be converted to a binary number.
If you get used to this conversion method, you can calculate quickly.
Decimal to Octal, Decimal to Hex
Decimal to octal
To convert from decimal to octal, divide the decimal number by 8 and line up the remainders, then line up the remainders from bottom to top.
Example) (240) 10 → (360) 8 Base conversion.
(Note) (240) 10 represents decimal number 240.
Divide by 8 and list the remainders from the bottom up.

Decimal to Hexadecimal
To convert from decimal to octal, divide the decimal number by 8 and line up the remainders, then line up the remainders from bottom to top.
Example) (240) 10 → (F0)16 Base conversion.
(Note) (240) 10 represents decimal number 240.
Divide by 16 and list the remainders from the bottom up.

octal to decimal, hexadecimal to decimal
Octal to Decimal
Octal weights are shown below.
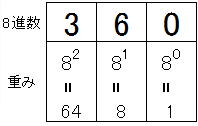
(360) 8
= 3 x 82 + 6 x 81 + 0 x 80
= 192 + 48 + 0
= (240) 10
Hexadecimal to Decimal
The hexadecimal weights are shown below.
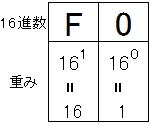
(F0) 16
= 15 × 16 1 + 0 × 16 0
= 240 + 0
= (240) 10
Binary to Octal, Binary to Hex
Binary to octal
Divide into three digits from the right. Fill in the gaps with 0.
(11110000) 2
= ( 0 11 110 000) 2 ← Divide into 3 digits from the right.
= (3 6 0) 8
= (360) 8
Binary to octal
Divide into four digits from the right. Fill in the gaps with 0.
(111110000) 2
= (000 1 1111 0000) 2 ← Divide into 4 digits.
= (1 F 0) 16
= (1F0) 16
Octal to Hex, Hex to Octal
Octal to hexadecimal
(360) 8
= (3 6 0) 8
= (011 110 000) 2 ← Convert each digit to binary number.
= (0 000 1111 0000) 2 ← Divide into 4 digits. Fill in the gaps with 0.
= (1111 0000) 2 ← Ignore high-order zeros.
= (F0) 16
= (F0) 16
Octal to hexadecimal
(F0) 16
= (F0) 16
= (1111 0000) 2 ← Convert each digit to binary number.
= (011 110 000) 2 ← Divide into 3 digits. Fill in the gaps with 0.
= (3 6 0) 8
= (360) 8
Subnet mask and binary number
In the world of networks, it has become the de facto standard to communicate using IP addresses.
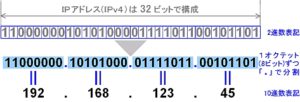
This IP address is expressed as “xxx.xxx.xxx.xxx”, where “xxx” is a combination of four decimal numbers “0 to 255”. For example, “192.168.1.1”.
In some cases, this decimal IP address must be interpreted in binary.
Working with IP addresses means that you will frequently be calculating binary to decimal conversions and vice versa.
For example, when converting the binary number below to a decimal number, it cannot be said that the efficiency is good if it is calculated as below.
(11110000) 2
= 1 x 27 + 1 x 26 + 1 x 25 + 1 x 24
+ 0 x 2 3 + 0 x 2 2 + 0 x 2 1 + 0 x 2 0
= 128 + 64 + 32 + 16 + 0 + 0 + 0 + 0
= (240) 10
IP address calculations often use a value called a subnet mask. If you memorize the numbers used in the subnet mask below, the calculation will be very easy.
*The meaning of the subnet mask will be introduced in a later content.
(11111111) 2 = (255) 10
(11111110) 2 = (254) 10
(11111100) 2 = (252) 10
(11111000) 2 = (248) 10
(11110000) 2 = (240) 10
(11100000) 2 = (224) 10
(11000000) 2 = (192) 10
(10000000) 2 = (128) 10
(00000000) 2 = (0) 10
Also, if you memorize the above numbers, it will be easy to convert 193 to binary, for example.
193 = 192 + 1
if you memorize 192
(11000000) 2 + (00000001) 2 = (11000001) 2
can be obtained immediately by calculating.